
By Harvey Sapigao
IMAGINE yourself standing on a concrete floor. Your goal is to cover the floor with red and blue square tiles completely, but in a way that follows three rules:
1) Every time you step on a tileless area, you must lay a tile. You can place either a red or blue tile on your starting position.
2) When you move one step horizontally or vertically, you must place a tile that is not the same color as the one you left. For example, if you started on a red tile and moved right, left, up, or down, lay a blue tile on your new location.
3) When you move one step diagonally, you must place a tile with a similar color to the tile you left. If you were standing on a red tile and moved diagonally, lay a red tile.
Once you have covered the floor with tiles, you will have created a colored checkerboard pattern. More interestingly, you will have also created a 2D model for the structure of salt crystals, which consists of alternating sodium and chlorine atoms: Red tiles can represent sodium atoms, while blue tiles can represent chlorine atoms.
Coloring a pattern such as the checkerboard is simple, but it becomes more complicated as patterns become more intricate. Dr. Allan Junio of the UP Diliman College of Science Institute of Mathematics (UPD-CS IM) created a technique that systematically colors patterns, helping model the structures of crystals.
Much like the three-step process in tiling the floor, Dr. Junio’s technique involves a set of general mathematical rules, called theorems and lemmas, in coloring different patterns. Moreover, his method enumerates all possible ways a pattern can be colored while limiting the number of colors used.
“The reason for this restriction is that we will be applying the coloring framework on the atoms of crystal structures, where the colors correspond to exactly one kind of atom, and we will be dealing with crystal structures with only finitely many kinds of atoms,” Dr. Junio explained in his paper.
The technique can help model a process called ordered substitution, where a group of atoms are replaced with a different element, thereby deriving a new material.
To demonstrate, he applied his technique to sphalerite crystal – a mineral that is difficult to identify due to its similarity with other crystals, hence its name coming from the Greek word sphaleros, meaning “treacherous.” Sphalerite is commonly made up of zinc and sulfur atoms linked together in a pattern.
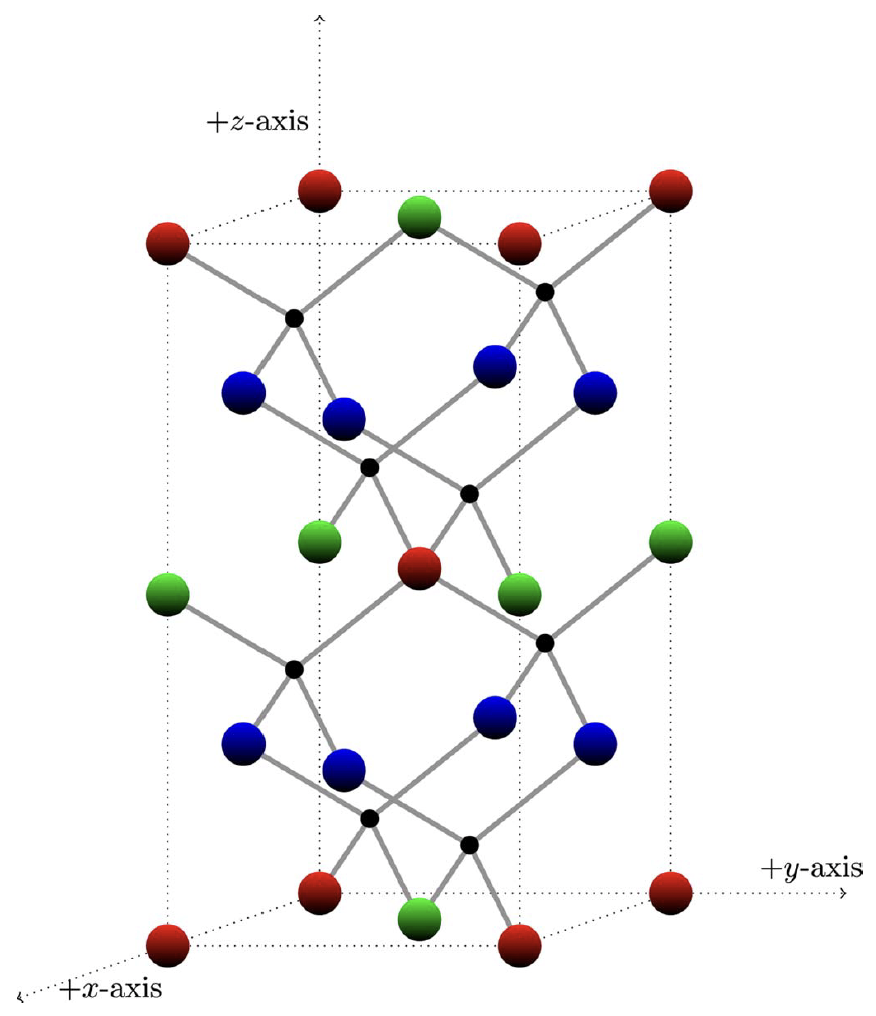
Instead of representing all zinc atoms with only one color, he colored different groups with green, red, and blue. In doing so, ordered substitution becomes simpler: by replacing the blue zinc atoms with copper atoms, the green zinc atoms with iron atoms, and the red zinc atoms with tin atoms, a new material called stannite is produced. Other crystals such as kuramite and chalcopyrite can also be produced using a similar process.
Although only sphalerite and its derivatives are modeled in the paper, the technique can be applied to other crystals as well.
“It may be a good idea to determine whether the resulting colorings correspond to known compounds, and if no such compounds exist, to establish whether the colorings may be realized as physical structures using chemical and molecular properties and restrictions,” Dr. Junio concluded in his paper, which is now published in Acta Crystallographica.
Reference:
Junio, A. O. (2023). Colorings of patterns fixed by an arbitrary finite-index subgroup of the Symmetry Group. Acta Crystallographica Section A Foundations and Advances, 79(6), 550–559. https://doi.org/10.1107/s2053273323007878



